PRML 8.3.3 Image De-Noisingやってみた
Pattern Recognition and Machine Learning (PRML) 第8章 Graphical Modelsを読んでいます。ネットワークを図で理解できるのはいいですが、これまでの章と毛並みが違っていて取っ付きにくいかも。モデルの目的や意義が抽象的にしか説明されておらず、何の役に立つのだろうと疑問に思いつつ読み続けるのは正直辛いものがあります。64頁もあるし。ところでこの章は "Baysian networks" だとか "Markov random fields" だとか役者の名前がいちいちかっこいいですね。一方、第6章の "Gaussian processes" や "kernel trick" は何故か癇に障りました(八つ当たり)。
第8章を苦労して読んでいる中、8.3.3の画像ノイズ除去は話が具体的で分かりやすく、砂漠の中でオアシスを見つけたように感じられました。正直それまでのストーリーとあまりつながってる気がしないのだけど。教科書の手法をPythonで再現してみます。
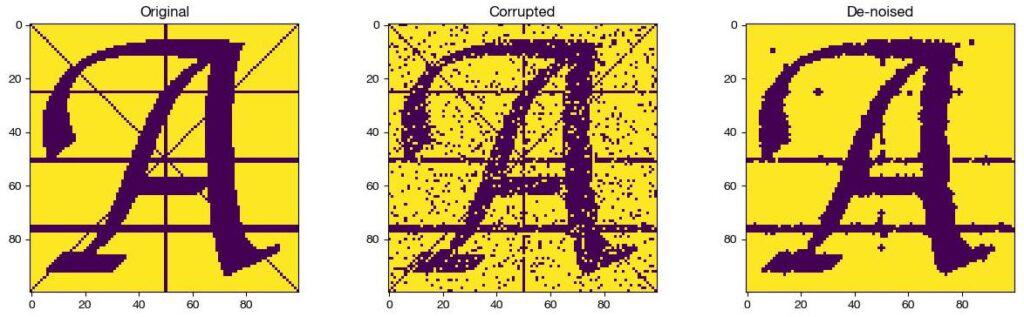
先ず白黒画像のNumpyデータを読み込みます。縦100 px ✕ 横100 px、白: 1, 黒: -1、縦線と斜線は太さ1 px、横線は上から1 px, 2 px, 3 pxです。教科書は元の画像もノイズ追加画像からの推定も\(x\)と表記していますが、ここでは元の画像データをimg、ノイズ追加画像からの推定を\(x\)と区別します。
from matplotlib import pyplot as plt
import numpy as np
img = np.load('A.npy')
height, width = img.shape
次に画像にノイズを追加します。
p = 0.1
# ノイズ生成
noise_ = np.ones(width * height, dtype="int8")
noise_[: int(p * width * height)] = -1
np.random.shuffle(noise_)
noise = noise_.reshape(height, width)
# 画像にノイズ追加
y = img * noise
ではいよいよiterated conditional modes (ICM) によりエラー関数 (8.42) を最小化します。 \[E(x,y)=h\sum_i {x_i} -\beta\sum_{{i, j}}x_ix_j-\eta\sum_i x_iy_i \tag{8.42}\] 本文にある通り、1ピクセルごとローカルに処理していきます。エラー関数の値に影響を与えるのは\(x_i\)と隣接\(x_j\) 8ピクセルの計9ピクセルのみなのでその部分を取り出して \[E_i=h x_i-\beta x_i \sum_{j \neq i}{x_j} -\eta x_i y_i\]
ここでパラメータ\(h, \beta, \eta\)の解釈は
- \(h\) : 画像の明暗調整。\(h>0\) 黒増強、\(h<0\) 白増強。
- \(\beta\) : \(x_i\)の隣接8ピクセル(\(x_i\)が画像の端の場合3ないし5ピクセル)の\(x_j\)の平均に\(x_i\)を引き寄せる。
- \(\eta\) : ノイズ追加画像データ\(y\)からの変更に対するペナルティ。
\(x_i\)の符号を反転させると\(E_i\)は絶対値が変わらず符号が反転します。当然、\(E_i>0\) なら\(x_i\)の符号を反転させた後の\(E_i\)の方が小さいし、\(E_i< 0\) なら\(x_i\)の符号を反転させると\(E_i\)が大きくなります。結局\(E_i\)の符号が正の時のみ\(x_i\)の符号を反転させればよいということになります。
h, beta, eta = 0, 1.0, 2.1
x = y.copy()
# ノイズ除去
count = 0
while True:
x_prev = x.copy()
for i0 in range(height):
for i1 in range(width):
xi =x[i0, i1]
Ei = h*xi -beta*xi*np.sum(x[max(i0-1,0):i0+2, max(i1-1,0):i1+2]) -xi) -eta*xi*y[i0,i1]
if Ei > 0:
x[i0, i1] = - xi
if np.all(x == x_prev):
break
else:
count += 1
print(f'converged in {count} rounds')
# 描画
fig = plt.figure()
ax = fig.add_subplot(1, 3, 1)
ax.imshow(img)
ax = fig.add_subplot(1, 3, 2)
ax.imshow(y)
ax = fig.add_subplot(1, 3, 3)
ax.imshow(x)
数回のループで収束し、こうなります。アルゴリズムから予想されることですが、太さ1ピクセルの線は隣接ピクセルの値に引き寄せられ消えてしまっています。