衆院選の当落が明らかになっていく様を確率論的にシミュレーションする
BishopのPattern Recognition and Machine Learning (PRML) 第2章 Probability Distribution から2.2.1 The beta distributionを取り上げ、選挙開票の次第に勝負が明らかになっていく過程をシ ミュレーションします。ベータ分布とは\[\rm{Beta} (\mu | {\it a}, {\it b} ) = {\rm{\Gamma} ( {\it a} + {\it b} ) \over \rm{\Gamma} ( {\it a} ) \rm{\Gamma} ( {\it b} )} \mu^{{\it a}-1} (1-\mu) ^{{\it b}-1} \tag{2.13}\]
\[\rm{\Gamma} ( {\it x} ) = \int_{0}^{\infty} {\it u}^{{\it x} - 1} e^{-{\it u}} {\it du} \tag{1.141}\]で表される確率分布であり、二項分布の共役事前分布としての性質を持っています。数式の見た目がおっかないですが、Scipyのscipy.stats.beta関数を用いて分布を簡単に求めることができます。
2021年衆議院選挙の際、東京1区にて自民党山田氏が立憲民主党海江田氏に競り勝ちしました。開票結果は次の通りです。
| 政党 | 候補者 | 得票数 |
| 自由民主党 | 山田美樹 | 99,133 |
| 立憲民主党 | 海江田万里 | 90,043 |
| 日本維新の会 | 小野泰輔 | 60,230 |
| 無所属 | 内藤久遠 | 4,715 |
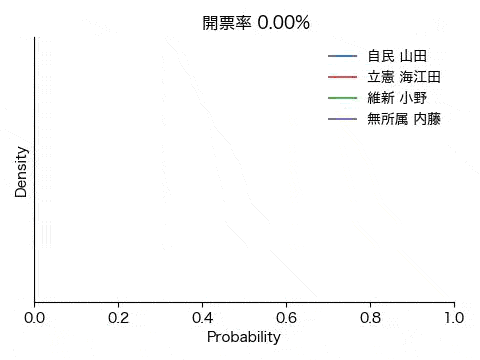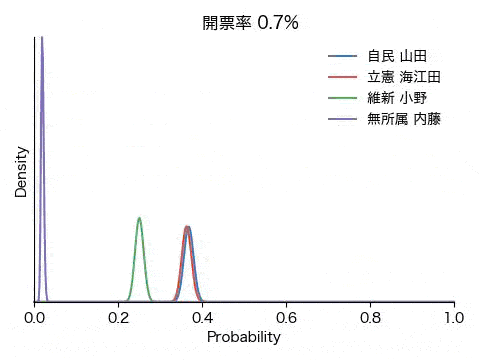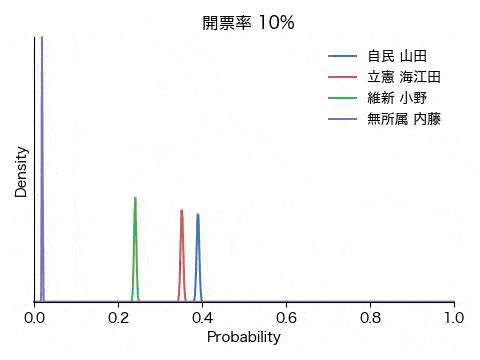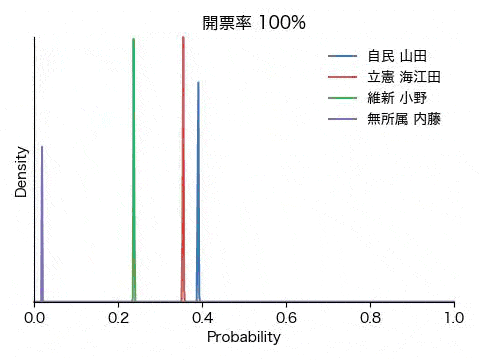
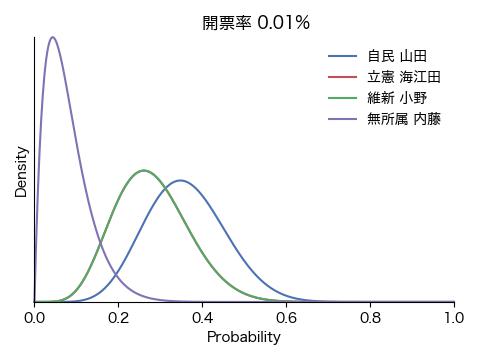
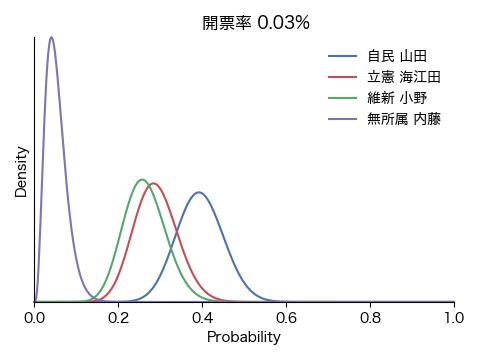
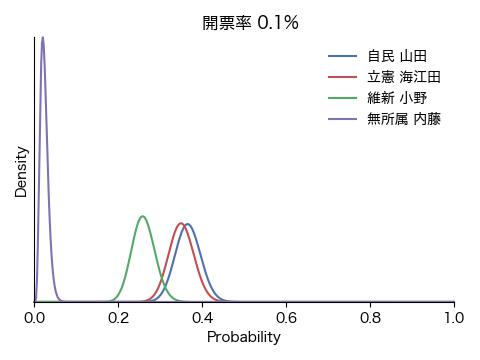
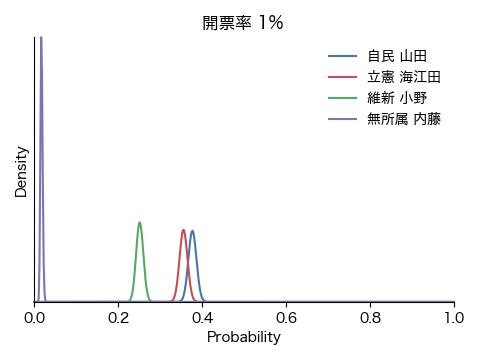
ここでは、得票数に等しい数のラベルの配列を作成しシャッフルすることにより開票過程をシミュレーションします。各候補者にとってそれぞれの投票用紙は自分の得票かそうでないかの2通りなので、ベータ分布に当てはめます。こうして逐次、各人の得票率の確からしさを求め、どの時点で勝利|敗北宣言を出せる雰囲気になるか、固唾を呑んで(嘘)見守ります。
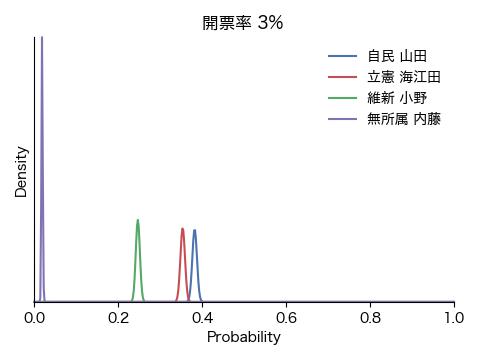
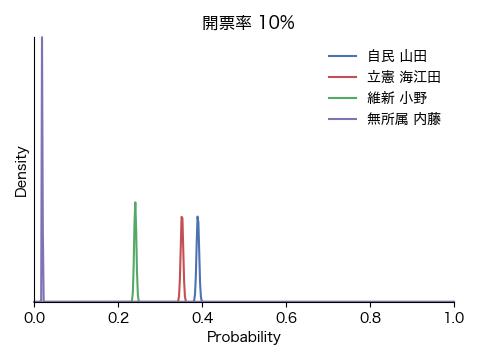
結果は冒頭のアニメGIFと下の図の通りです。ごく初期にこそ戦況が混沌としているものの、開票率0.1%の段階で内藤氏に勝ち目がないことが明確になり、次いで開票率1%前後で小野氏が脱落、接戦が予想された山田氏と海江田氏の勝敗も開票率3%の時点で既に決していることが分かります。
%matplotlib widget
from matplotlib import pyplot as plt
from matplotlib import rcParams
import random
from scipy.stats import beta
n_votes = {"自民 山田": 99133,
"立憲 海江田": 90043,
"維新 小野": 60230,
"無所属 内藤": 4715}
totalvotes = sum(n_votes.values())
# 票のリストを作りランダムに並べて投票箱を模す。
votes = [key for key, value in n_votes.items()
for i in range(value)]
random.shuffle(votes)
def plot_prob_density(ax, percent_counted):
# percent_counted: 開票率
U = np.linspace(0, 1, 500)
n = int(percent_counted / 100 * totalvotes) # 開票数
A = [votes[:n].count(key)
for key in n_votes.keys()] # 現時点の各候補得票数
P = [beta.pdf(U, a, n - a) for a in A] # 各人の確率分布
# 描画
lines=ax.plot(U, P[0], "b-",
U, P[1], "r-",
U, P[2], "g-",
U, P[3], "m-")
ax.set_ylim(0, max([p.max() for p in P]))
if percent_counted < 0.1:
title = ax.set_title(f"開票率 {percent_counted:0.2f}%", loc="left", x=0.4)
elif percent_counted < 1:
title = ax.set_title(f"開票率 {percent_counted:0.1f}%", loc="left", x=0.4)
else:
title = ax.set_title(f"開票率 {percent_counted:0.0f}%", loc="left", x=0.4)
plt.tight_layout()
return lines # 確率分布曲線だけ消去し更新できるようハンドルを返す
%matplotlib inline
# 図の作成
figsize = (4.8, 3.6)
rcParams["axes.spines.left"] = True
fig = plt.figure(figsize=figsize)
ax = fig.add_subplot()
ax.tick_params(left=False, labelleft=False)
ax.set_xlim(0, 1)
ax.set_xlabel("Probability")
ax.set_ylabel("Density")
# レジェンドを作るためのダミーのプロット
dummyxy = [-2, -1]
ax.plot(dummyxy, dummyxy, "b-", label=list(n_votes.keys())[0])
ax.plot(dummyxy, dummyxy, "r-", label=list(n_votes.keys())[1])
ax.plot(dummyxy, dummyxy, "g-", label=list(n_votes.keys())[2])
ax.plot(dummyxy, dummyxy, "m-", label=list(n_votes.keys())[3])
ax.legend()
# ある開票率(percent_counted)の時点の確率分布をプロット
lines = plot_prob_density(ax, percent_counted=1)
# 確率分布曲線を消去するには↓
for line in lines:
line.remove()

